¶ 应试
还是有同学问考试复习的重点内容,其实我们上课的重点就是考试的重点,最后一次课也给大家做了一些总结,周三就考试了,再给大家强调一下重点的复习内容吧
老师原话((
顺序结构:
-
各种排序算法的思想、执行过程以及程序实现
基数排序、插入排序、冒泡排序、归并排序、选择排序、堆排序、快速排序
-
队列和栈中的入队出队入栈出栈顺序问题
-
给定程序的时间复杂度
-
Hash函数和线性探测执行过程以及查找一个元素需要比较的次数
-
线性结构不同存储形式的特点
-
几种特殊矩阵存储方式以及映射函数
-
Hash表和跳表存储方式和查找方式
层次结构:
- 任意给定两种二叉树的遍历序列可以画出二叉树
- 哈夫曼树和哈夫曼编码
- 最大堆和最小堆的概念以及插入删除元素的调整过程
- 二叉搜索树的概念以及查找、插入和删除节点的操作过程和程序实现过程
- 平衡二叉树的概念以及查找、插入和删除节点的操作过程等。
图结构:
- 给定图求解最小生成树的常用的两种算法思想以及求解过程
- 拓扑排序的思想和过程
- 动态规划中求最短路径的经典算法思路
- 设计动态规划算法解决实际问题的算法思路和程序实现
- 深度优先算法和广度优先算法的思想、过程和程序实现。
¶ 数据结构简介
数据结构包括三个方面:
- 逻辑结构:指从解决问题的需要出发,为实现必要的功能所建立的数据结构,它属于用户的视图,是面向问题的,表示数据元素之间的逻辑关系;
- 存储结构:是指数据如何在计算机中存放,是数据逻辑结构的物理存储映象,是属于具体实现的视图,是面向计算机的
- 运算:作用于数据结构上的运算,及实现方法(查找、插入、删除、更新等)
¶ 逻辑结构
数据的逻辑结构是指从解决问题的需要出发,为实现必要的功能所建立的数据结构,它属于用户的视图,是面向问题的(或者说是面向应用的)。
逻辑结构有三种:
- 线性结构
- 树形结构
- 网状(图)结构
¶ 存储结构
数据的存储结构是指数据如何在计算机中存放,是数据逻辑结构的物理存储映象,是属于具体实现的视图,是面向计算机的。
存储结构有:
- 顺序存储(公式化描述)
- 链式存储(链表描述)
- 索引存储(间接寻址)
- 模拟指针
- 散列存储
¶ 数组存储
线性表使用公式化描述方式存储。编写一个函数,从一给定的线性表A中删除值在x~y(x<=y)之间(包含x和y)的所有元素,要求以较高的效率来实现,并给出时间复杂度/删除重复元素:
使用两个指针,一个用于保存最近的有效元素,一个用于遍历;当符合条件指向有效元素的指针向后移动,否则停在第一个无效元素上,遍历指针一直遍历,直到出现新的符合条件的元素就将其交换。
¶ 算法简介
运算的定义直接依赖于逻辑结构,例如线性表、队列/堆栈、树、图;运算的实现依赖于存贮结构,例如顺序存储、链式存储。
¶ 程序性能分析
¶ 线性表
比较数组、链表和间接寻址的优缺点:
| 项目 | 数组 | 链表 | 间接寻址 | 备注 |
|---|---|---|---|---|
| 初始化 | 有确定的大小 | 动态分配内存 | 动态分配内存 | |
| 添加 | 数据增加时可能会超出原数组大小,需要扩充数组并将数据复制到新的数组里 | 存储数据的个数取决于数组的长度 | ||
| 删除 | 需要调整前一个元素的指针并释放被删除元素的内存空间 | 需要改变数组的指针,并释放被删除元素的 | ||
| 查找 | 可以通过映射公式直接访问 | 按顺序遍历 | 可以通过映射公式直接访问到指针,然后访问元素自身 | |
| 顺序读写 | 和数组相同 | |||
| 随机读写 | 无法实现高效的随机读写 | 能够实现随机读写 | ||
¶ 数组描述
数组描述的优点:
- 各种方法可以用非常简单的C++函数来实现。
- 执行搜索、删除和插入的两数都有一个最坏与表的大小呈线性关系的时间复杂性。
- 不需要为表示结点间的逻辑关系而增加额外的存储空间(存储密度高)
- 可以方便的随机存取表中的任一结点。
数组描述的缺点:
- 插入、删除元素需要移动表内数据。
- 空间需要事先申请,专用,空闲空间不能共享。
- 空间的低效利用。
数组的行、列主映射有一定规律:行主映射从前往后看,列主映射倒着看。
¶ 链表描述
优点:
- 插入、删除操作的时间复杂性不依赖于元素大小
- 插入、删除元素不需要移动表内数据
- 空间不需要事先申请
缺点:
- 每个节点中需要额外的空间用于保存链接指针
- 不能随机存取表中的任一节点
- 如果数据有序,可使用折半搜索
¶ 模拟指针
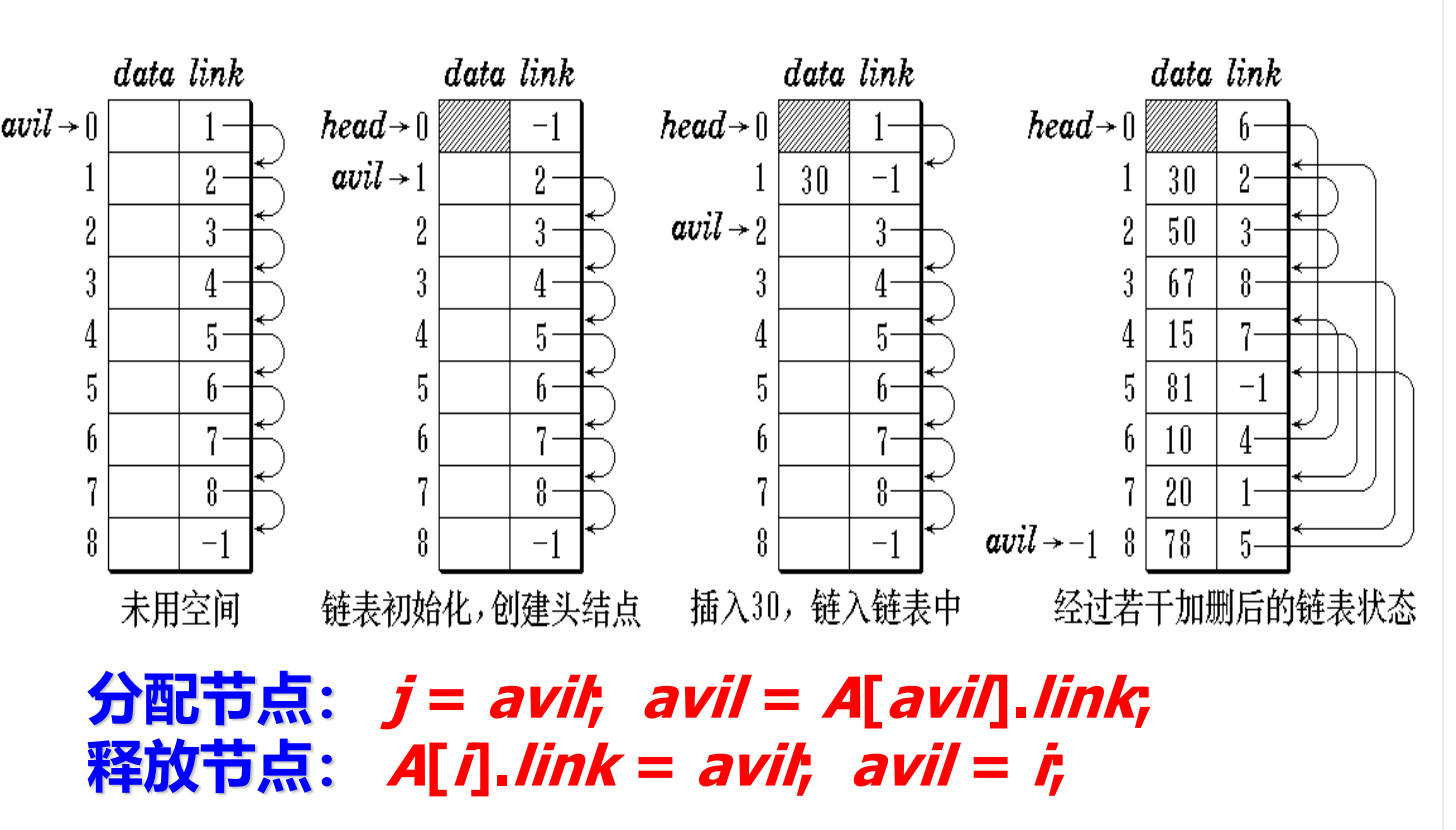
采用一个节点数组以及对该数组进行索引的模拟指针,可以使设计更方便、更高效。
¶ 间接寻址
在间接寻址方式中,使用一个指针表来跟踪每个元素。可采用一个公式水定位每个指针的位置,以便找到所需要的元素。元素本身可能存储在动态分配的节点或节点数组中。
¶ 数组与矩阵
¶ 矩阵的映射设计
¶ 稀疏矩阵
对一个大小为 的矩阵。
转置复杂度为
加法复杂度为
¶ 特殊矩阵
- 对角矩阵:使用一个长度为
n的一维数组 - 三对角矩阵:使用一个长度为的数组来保存,可以按照行主映射、列主映射和对角映射。
- 三角矩阵:使用长度为\frac{n(n+1)}
- 对称矩阵:只存储矩阵的上三角或下三角
¶ 三对角矩阵
对角映射:按从下往上的顺序映射三个对角线。
对角线映射公式:
¶ 等对角矩阵(Chapter7.36)
一个nxn的矩阵T称为等对角矩阵(Toeplitz matrix),当且仅当心1和,1时,T()= T(i-1,/-1)。
1)证明一个nx/的等对角矩阵最多有 2n-1个不同的元素。
2)设计一个映射,把一个等对角矩阵映射到一个长度为 2n-1 的一维数组。
3)采用2)的映射模式设计一个 C++类 toeplitzMatrix,用一个大小为 2n-1 的一维数组来存储等对角矩阵。包含 get 和 set 方法。这两个方法的时间复杂度应为 0(1)。
4)编写一个成员方法,实现以2)方式存储的两个等对角矩阵的乘法,结果存储在一个二维数组。确定时间复杂度。
¶ 栈
¶ 基本定义
栈是 OI 中常用的一种线性数据结构,请注意,本文主要讲的是栈这种数据结构,而非程序运行时的系统栈/栈空间。
栈的修改是按照后进先出的原则进行的,因此栈通常被称为是后进先出(last in first out)表,简称 LIFO 表。
¶ 实现方式
可以通过数组和链表来模拟栈,例如使用C++的数组来模拟:
int st[N];
// 这里使用 st[0] (即 *st) 代表栈中元素数量,同时也是栈顶下标
// 压栈 :
st[++*st] = var1;
// 取栈顶 :
int u = st[*st];
// 弹栈 :注意越界问题, *st == 0 时不能继续弹出
if (*st) --*st;
// 清空栈
*st = 0;
也可以使用Go编写一个很简单的栈结构:
// declare a stack
type Stack struct {
Items []int
}
// push an item to the stack
func (s *Stack) Push(item int) {
s.Items = append(s.Items, item)
}
// pop an item from the stack
func (s *Stack) Pop() int {
item := s.Items[len(s.Items)-1]
s.Items = s.Items[:len(s.Items)-1]
return item
}
// check if the stack is empty
func (s *Stack) IsEmpty() bool {
return len(s.Items) == 0
}
// get the top item of the stack
func (s *Stack) Top() int {
return s.Items[len(s.Items)-1]
}
// get the size of the stack
func (s *Stack) Size() int {
return len(s.Items)
}
// print the stack
func (s *Stack) Print() {
fmt.Println(s.Items)
}
¶ 应用
栈几乎是使用最广泛的数据结构之一。
¶ 括号匹配
匹配一个字符串中的左、右括号。
判断 是否为合法括号序列的经典方法是贪心思想。该算法同样适用于变种括号序列。
我们维护一个栈,对于 依次考虑:
如果 是右括号且栈非空且栈顶元素是 对应的左括号,就弹出栈顶元素。
若不满足上述条件,则将 压入栈中。
在遍历整个 后,若栈是空的,那么 就是合法括号序列,否则就不是。时间复杂度 。
¶ 汉诺塔
// 利用栈实现汉诺塔
func hanoiTowerInStakc(n int) {
stacks := make([]Stack, 3)
for i := n; i > 0; i-- {
stacks[0].Push(i)
}
showStacks(stacks)
moveAndShow(stacks, n, 0, 1, 2)
}
func showStacks(stacks []Stack) {
for i := 0; i < len(stacks); i++ {
fmt.Printf("stack %d: ", i)
stacks[i].Print()
}
fmt.Println()
}
func moveAndShow(stacks []Stack, n, from, to, temp int) {
if n == 1 {
stacks[to].Push(stacks[from].Pop())
showStacks(stacks)
} else {
moveAndShow(stacks, n-1, from, temp, to)
stacks[to].Push(stacks[from].Pop())
showStacks(stacks)
moveAndShow(stacks, n-1, temp, to, from)
}
}
¶ 列车车厢重排
货运列车共有n节车厢,每节车厢将停放在不同的车站,n个车站的编号分别为1到n。货运列车按照第n站至第1站的次序经过这些车站,车厢的编号与它们的目的地相同。重新排列车厢,使各车厢从前至后按编号1到n的次序排列。
要解决这个问题需要使用若干“缓冲铁轨”,他们是按照LIFO方式使用的。也就是说当一个车厢进入轨道时,可以选择进入一个缓冲铁轨或者直接出轨。
火车进入缓冲轨道时,有这样的规则:
- ,其中是轨道内最顶部的车厢编号。由于LIFO的性质,这样才能保证小编号车厢先出去。
- 是满足条件的最小的缓冲轨道。
¶ 开关盒布线
¶ 离线等价类问题
详见并查集。
¶ 迷宫老鼠
¶ 队列
抽象类定义:
templae<class T>
class queue
{
public:
virtual ~queue() { }
virtual bool empty() const = true;
virtual int size() const = 0;
virtual T& front() = 0;
virtual T& back() = 0;
virtual void pop() = 0;
virtual void push(const T& thElement) = 0;
}
¶ 数组表示
¶ 直接表示
映射公式可以表示为:
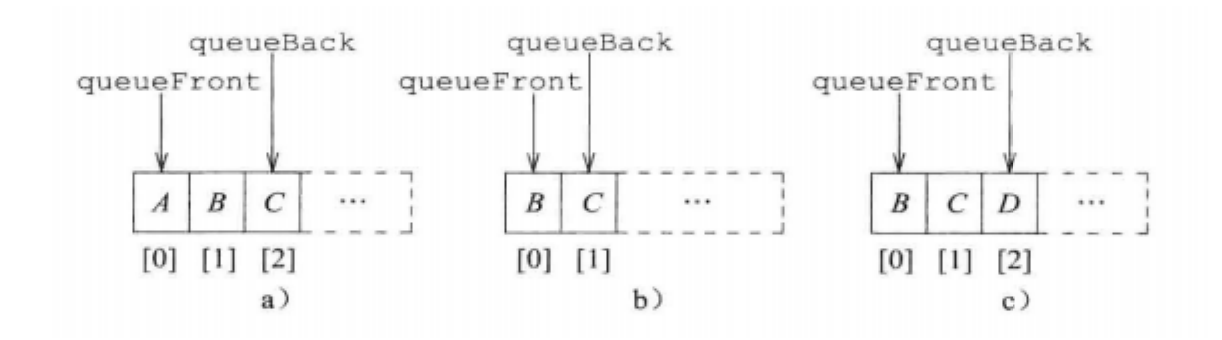
这会带来两个问题:每次删除后,需要将所有元素向前移动1个位置,因此出队的复杂度为 。
其queueFront总是为0,queueBack为最后一个元素的位置,empty的条件是queueBack = -1。
¶ 间接定位
映射公式从队列头开始映射:
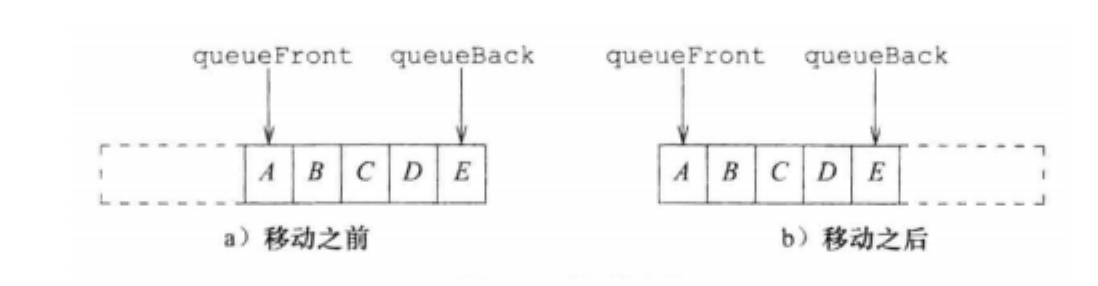
随之带来的问题是可能出现前半段为空后半段满的情况,这时候插入需要将所有元素移动到前面
empty()的条件为queueBack < queueFront。
¶ 循环队列
使用数组模拟队列会导致一个问题:随着时间的推移,整个队列会向数组的尾部移动,一旦到达数组的最末端,即使数组的前端还有空闲位置,再进行入队操作也会导致溢出(这种数组里实际有空闲位置而发生了上溢的现象被称为“假溢出”)。
循环队列将上一种映射方式首尾相接,映射公式变为:
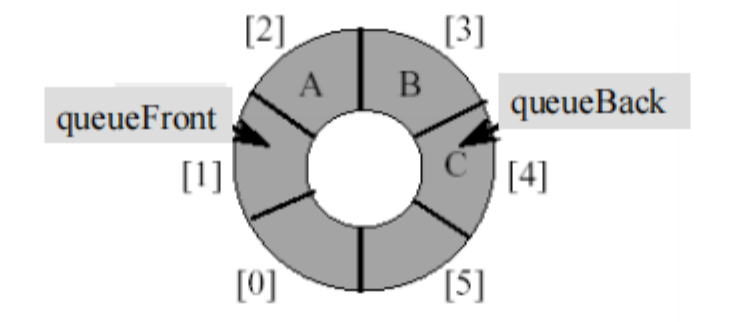
其queueFront指向队列首元素的下一个位置,queueBack指向最后一个元素的位置。
在这种情况下,判对列为空的条件是queueBack = queueFront。而队列满的条件同样为queueBack = queueFront。
因此此时队列不能填满,其有效长度只能为arrayLength - 1,这样的话队列满的条件则为(queueBack + 1) % arrayLength = queueFront。
¶ 链表表示
使用从头到尾的方式用链表构建队列:
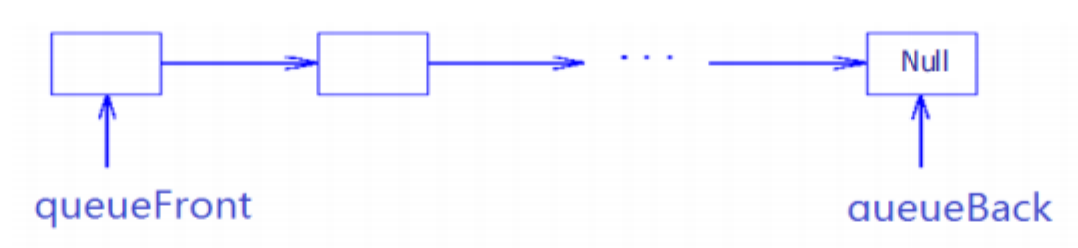
链表实现中,应该使用queueFront作为首指针,这样可以在出队的时候得到 的复杂度。
¶ 双端队列
双端队列是指一个可以在队首/队尾插入或删除元素的队列。相当于是栈与队列功能的结合。具体地,双端队列支持的操作有 4 个:
- 在队首插入一个元素
- 在队尾插入一个元素
- 在队首删除一个元素
- 在队尾删除一个元素
数组模拟双端队列的方式与普通队列相同。
¶ 应用
¶ 列车车厢重排
¶ 电路布线
¶ 识别图元
¶ 跳表和散列
Hash和跳表的优缺点:
| 项目 | Hash | 跳表 | 备注 |
|---|---|---|---|
| 复杂度 | |||
| 实现 | |||
| 查找 | Redis中的有序集合就是通过跳表实现的,而不是红黑树 | ||
| 插入 | 需要解决散列冲突的问题 | ||
| 删除 |
¶ 字典/哈希表/散列表
哈希表又称散列表,一种以「key-value」形式存储数据的数据结构。所谓以「key-value」形式存储数据,是指任意的键值 key 都唯一对应到内存中的某个位置。只需要输入查找的键值,就可以快速地找到其对应的 value。可以把哈希表理解为一种高级的数组,这种数组的下标可以是很大的整数,浮点数,字符串甚至结构体。
字典当然可以使用线性结构描述,这样对于顺序的输出是没有任何问题的,但是如果要进行随机读写就会有新的麻烦。
¶ 跳表
跳表 (Skip List) 是由 William Pugh 发明的一种查找数据结构,支持对数据的快速查找,插入和删除。跳表的期望空间复杂度为 ,跳表的查询,插入和删除操作的期望时间复杂度都为 。
准确地说,跳表是对有序链表的改进。一个有序链表的查找操作,就是从头部开始逐个比较,直到当前节点的值大于或者等于目标节点的值。很明显,这个操作的复杂度是 O(n)。
跳表在有序链表的基础上,引入了 分层 的概念。首先,跳表的每一层都是一个有序链表,特别地,最底层是初始的有序链表。每个位于第 层的节点有 的概率出现在第 层, 为常数。
记在 个节点的跳表中,期望包含 个元素的层为第 层,易得。
在跳表中查找,就是从第 层开始,水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层。重复这个过程直至到达第一层且无法继续进行操作。此时,若下一个节点是目标节点,则成功查找;反之,则元素不存在。这样一来,查找的过程中会跳过一些没有必要的比较,所以相比于有序链表的查询,跳表的查询更快。可以证明,跳表查询的平均复杂度为 。
¶ 跳表的随机访问优化
¶ 散列表(P246)
散列(Hashing) :字典的另一种描述方法就是散列.
散列方法:是用一个散列函数(hash function又称哈希函数)把字典的数对映射到散列表/哈希表(hash table)中的具体位置。
要让键值对应到内存中的位置,就要为键值计算索引,也就是计算这个数据应该放到哪里。这个根据键值计算索引的函数就叫做哈希函数,也称散列函数。在实际的应用中,键值可能是更复杂的东西,比如浮点数、字符串、结构体等,这时候就要根据具体情况设计合适的哈希函数。哈希函数应当易于计算,并且尽量使计算出来的索引均匀分布。
¶ 冲突和溢出
如果对于任意的键值,哈希函数计算出来的索引都不相同,那只用根据索引把 (key, value) 放到对应的位置就行了。但实际上,常常会出现两个不同的键值,他们用哈希函数计算出来的索引是相同的。存储桶中若没有空间时就发生溢出。
当每个桶只能存储一个数对时,碰撞和溢出会同时发生
- 线性探查:当溢出发生时,将元素插入下一个可用桶中。在寻找下一个可用桶时,表被视为环形的。
- 链式散列
线性探查(线性开型寻址、开放寻址法)的思路如下:
-
插入:
# 计算f(k) # 检查list[f(k)]是否为空,否则向后移动直到一个空桶 # list[f(k) + m] = k -
查找:
# 计算f(k) # f(k) ?= k,若否则向后移动,直到 # 1. f(k) = k # 2. 遇到一个空桶 # 3. 回到起始桶 # 返回结果或者数据不存在 -
删除:
# 查找 # list[f(k)] ?= f(k),若是,直接删除 # 若不是,先删除,然后向后移动并判断 list[f(k) + m] ?= f(k),若是则向前移动,直到一个空桶或初始桶
¶ LZW压缩
基于原始数据,创建一个字典,字典中所存放的是文本中的字符串与其编码的映射。然后,用字典中的编码来代替原始数据中的相应字符串。
LZW规则:
- 开始,为该文本文件中所有可能出现的字母分配一个代码,构成初始字典。
- LZW压缩器不断地在输入文件的未编码部分中寻找在字典中出现的最长的前缀p,输出前缀p相应的代码,若输入文件中的下一个字符为c,则为pc分配一个代码,并插入字典。
¶ 二叉树
¶ 树的基本概念和描述
线性数据结构和表数据结构一般不适合于描述具有层次结构的数据。
- 树(tree)t是一个非空的有限元素的集合。
- 其中一个元素为根(root)。
- 其余的元素(如果有的话)组成t的子树(subtrees).
级(level)/层次:指定,其孩子(如果有)的级为2。
二叉树的高度(height)或深度(depth)是指该二叉树的级数(或层数)。
元素的度(Degree of an element) 是指其孩子的个数。树的度(The degree of a tree) 是其元素度的最大值。
¶ 二叉树和树的区别
二叉树( binary tree) 是有限个元素的集合(可以为空)。
- 二叉树可以为空,但树不能为空。
- 二叉树中每个元素都恰好有两棵子树(其中一个或两个可能为空)。而树中每个元素可有任意多个子树。
- 在二叉树中每个元素的子树都是有序的,也就是说,可以用左、右子树来区别。而树的子树间是无序的。
一棵度为2的树和一棵二叉树的区别:
- 度为2的树要求每个节点最多只能有两棵子树,并且至少有一个节点有两棵子树。二叉树的要求是度不超过2,节点最多有两个叉,可以是1或者0。
- 度为2的树有两个分支,但分支没有左右之分;一棵二叉树也有两个分支,但有左右之分,左右子树的次序不能随意颠倒。
- 度为2的树从形式上看与二叉树很相似,但它的子树是无序的,而二叉树是有序的。即,在一般树中若某结点只有一个孩子,就无需区分其左右次序,而在二叉树中即使是一个孩子也有左右之分。
¶ 二叉树的性质
- 包含n个元素的二叉树的边数为n-1
- 若二叉树的高度为h,则这棵树最少有h个元素,最多有2^h-1个元素
- 若二叉树包含的元素个数为n,则这棵树高度最小为[log2(n+1))],最大为n
当高度为h的二叉树恰好有2^h-1个元素时,称其为满二叉树(full binary tree)。
从满二叉树中删除k个元素,其编号为2^h-i, 1≤i≤k,所得到的二叉树被称为完全二叉树(complete binary tree)。
满二叉树是完全二叉树的一个特例。

¶ 二叉树的遍历
许多二叉树操作是通过对二叉树进行遍历来完成。在二叉树的遍历中,每个元素都被访问到且仅被访问一次。
在访问时执行对该元素的相应操作(复制、删除、输出等)。
有四种遍历二叉树的方法:前序遍历、中序遍历、后序遍历、逐层遍历。
中序遍历+前序/后序遍历,就可以画出一个二叉树。
具体来讲,首先通过在前序、后序序列中找到最前面、最后面的元素作为根节点,并以该元素区分中序序列的两侧,分别是左右两颗子树;按照这个方式递归就可以画出整个二叉树。
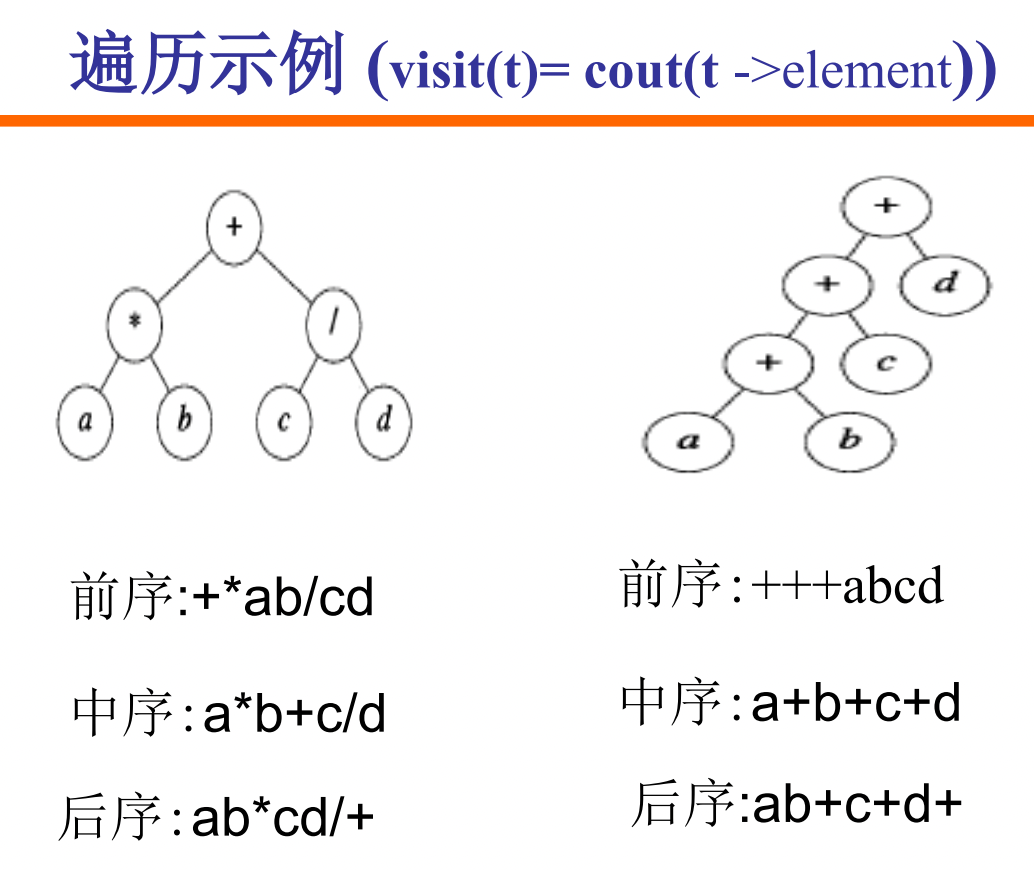
对于表达式二叉树,我们将得到的三种序列分别称为表达式的前缀、中缀和后缀形式。
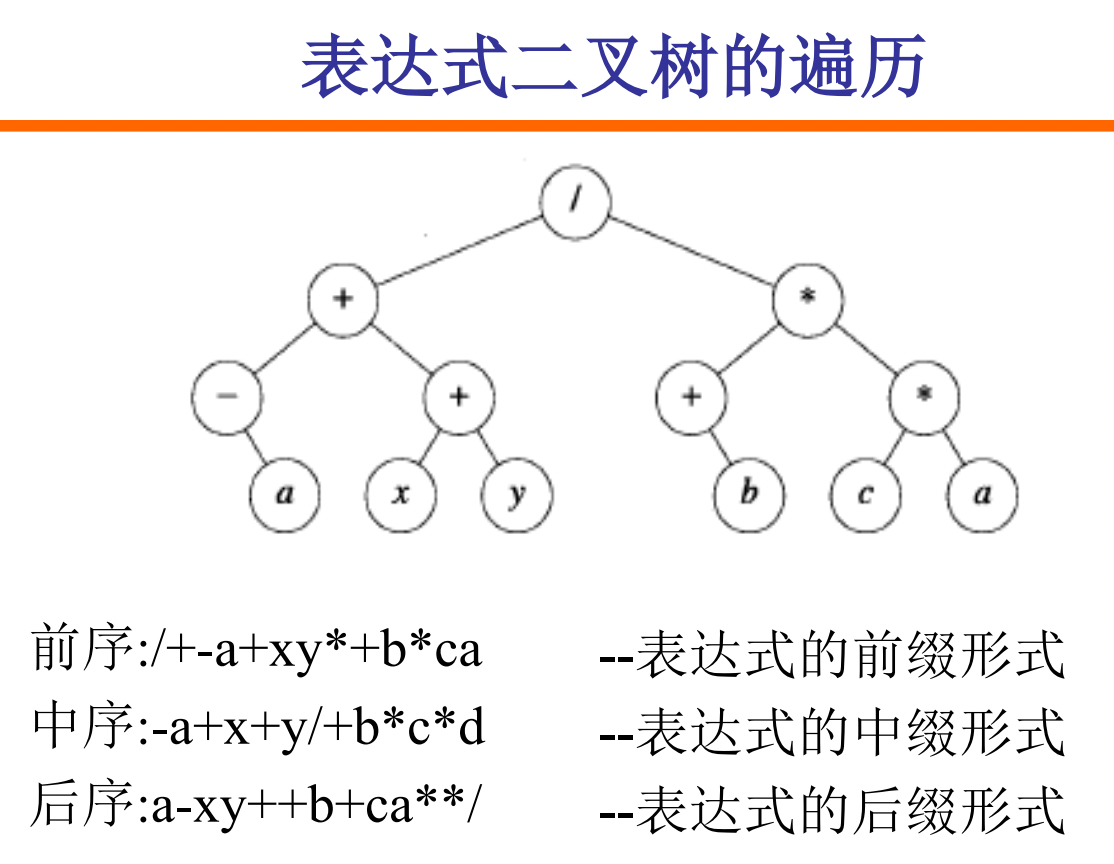
表达式的中缀形式存在歧义,通常使用后缀形式配合栈进行计算。
¶ 前序遍历
template <class E>
void preOrder(binaryTreeNode<E> *t)
{ //前序遍历二叉树*t
if (t != NULL)
{
visit(t); //访问根节点
preOrder(t->leftChild); //前序遍历左子树
preOrder(t->rightChild); //前序遍历右子树
}
}
非递归实现:
template <class T>
void PreOrder(binaryTreeNode<T> *t) //对*t进行前序遍历
{
stack<binaryTreeNode<T> *> s(MaxLength);
binaryTreeNode<T> *p = t;
do
{
while (p)
{
// 先访问每一个根结点
Visit(p);
s.push(p);
p = p->LeftChild;
}
if (!s.IsEmpty())
{
p = s.top();
s.pop();
p = p->RightChild;
}
} while (p || !s.IsEmpty())
}
¶ 中序遍历
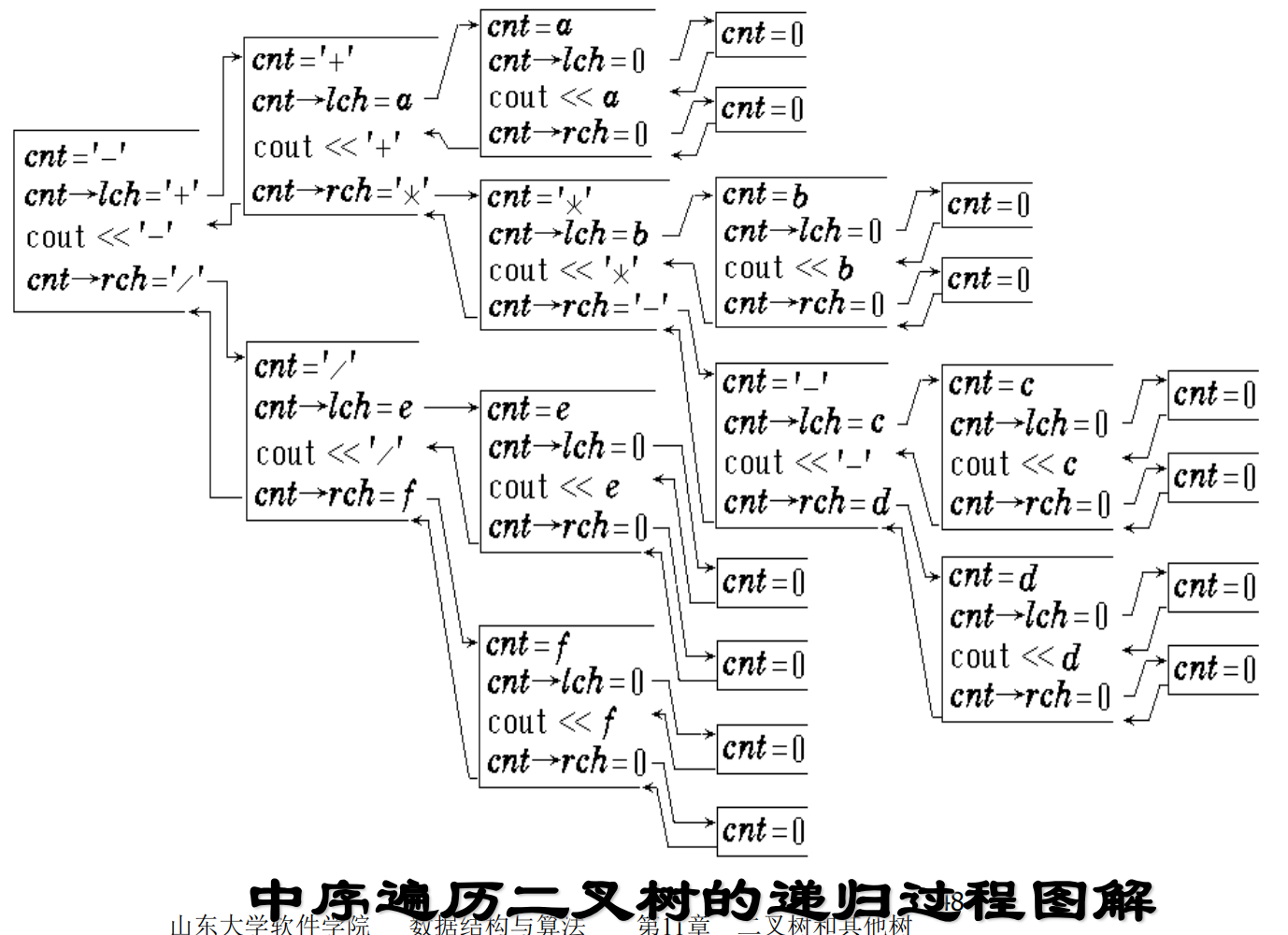
template <class E>
void inOrder(binaryTreeNode<E> *t)
{ //中序遍历二叉树*t
if (t != NULL)
{
inOrder(t->leftChild); //中序遍历左子树
visit(t); //访问根节点
inOrder(t->rightChild); //中序遍历右子树
}
}
非递归实现:
template <class T>
void InOrder(binaryTreeNode<T> *t) //对*t进行中序遍历
{
// 使用一个栈保存访问信息
stack<BinaryTreeNode<T> *> s(MaxLength);
BinaryTreeNode<T> *p = t;
do
{
// 先将所有的根🪢点入栈
while (p)
{
s.push(p);
p = p->LeftChild;
}
// 逐个取出根结点,先访问左子树再访问右子树
if (!s.IsEmpty())
{
p = s.top();
s.pop();
Visit(p);
p = p->RightChild;
}
} while (p || !s.IsEmpty())
}
¶ 后序遍历
template <class E>
void postOrder(binaryTreeNode<E> *t)
{ //后序遍历二叉树*t
if (t != NULL)
{
postOrder(t->leftChild); //后序遍历左子树
postOrder(t->rightChild); //后序遍历右子树
visit(t); //访问根节点
}
}
非递归实现:
template <class T>
void PostOrder(binaryTreeNode<T> *t) //对*t进行中序遍历
{
stack<binaryTreeNode<T> *> s(MaxLength);
int flag;
stack<int> flagStack; //存放标志位的栈,每出(入)一个节点指针,同步出(入)
binaryTreeNode<T> *p = t;
do
{
while (p)
{
s.push(p);
flagStack.push(1);
p = p->LeftChild;
}
if (!s.IsEmpty())
{
p = s.top();
flag = flagStack.top();
if (p->RightChild && flag == 1)
{
flagStack.pop();
flagStack.push(2);
p = p->RightChild;
}
else
{
s.pop();
flagStack.pop();
Visit(p);
p = 0;
}
}
} while (p || !s.IsEmpty())
}
¶ 层次遍历
template <class E>
void levelOrder(binaryTreeNode<E> *t)
{ //层次遍历二叉树*t
arrayQueue<binaryTreeNode<E> *> q;
while (t != NULL)
{
visit(t); //访问t
//将t的左右孩子放入队列
if (t->leftChild)
q.push(t->LeftChild);
if (t->rightChild)
q.push(t->rightChild);
try
{
t = q.front();
} //访问下一个节点 .
catch (queueEmpty)
{
return;
}
q.pop();
}
}
非递归实现:
template <class T>
void LevelOrder(T a[], int last)
{
// Level-order traversal of a binary tree.
LinkedQueue<int> Q;
if (!last)
return; // empty tree
int i = 1;
// start at root
while (true)
{
Visit(a, i);
// put children on queue
if (2 * i <= last && a[2 * i])
Q.Add(2 * i); // add left child
if (2 * i + 1 <= last && a[2 * i + 1])
Q.Add(2 * i + 1); // add right child
// get next node to visit
try
{
Q.Delete(i);
}
catch (OutOfBounds)
{
return;
}
}
}
¶ 二叉树的存储结构
- 数组表示:适合表达比较满的二叉树(完全二叉树/满二叉树)
- 链表表示:
¶ 二叉树的数组表示
二叉树的数组表示将二叉树表示为缺少了部分元素的完全二叉树。
¶ 二叉树的链表表示
节点定义:
template<class T>
struct binaryTreeNode
{
T element;
binaryTreeNode<T> * leftChild, rightChild;
binaryTreeNode() {leftchild = rightChild = nullptr;}
binaryTreeNode(const T& theElement) {
this.element(theElement);
leftChild = rightChild = nullptr;
}
binaryTreeNode(const T& theElement,
binaryTreeNode *theLeftChild,
binarytreeNode *theRighChild) {
this.element(theElement);
leftchild = theLeftChild;
rightChild = theRightChild;
}
}
¶ 二叉树的编写
基本内容:
template <class E>
class linkedBinaryTree:public binaryTree<binaryTreeNode<E>>
{
public:
linkedBinaryTree()
{
root = NULL;
treeSize = 0;
};
~BinaryTree(){erase()};
bool empty() const { reurn treeSize == 0; }
void preOrder(void (*theVisit)(binaryTreeNode<E> *))
{
visit = theVisit;
preOrder(root);
}
void inOrder(void (*theVisit)(binaryTreeNode<E> *))
{
visit = theVisit;
inOrder(root);
}
void postOrder(void (*theVisit)(binaryTreeNode<E> *))
{
visit = theVisit;
postOrder(root);
}
void levelOrder(void (*)(binaryTreeNode<E> *));
void erase();
{
postOrder(dispose);
root = NULL;
treeSize = 0;
}
private:
binaryTreeNode<E> *root; //根节点指针
int treeSize; //数的元素个数
static void (*visit)(binaryTreeNode<E> *); //访问函数
static void preOrder(binaryTreeNode<E> *t);
static void inOrder(binaryTreeNode<E> *t);
static void postOrder(binaryTreeNode<E> *t);
static void dispose(binaryTreeNode<E> *t){delete t}; //删除t指向的节点
}
¶ 遍历
template <class E>
void linkedBinaryTree<E>::preOrder(binaryTreeNode<E> *t)
{ //前序遍历二叉树*t
if (t != NULL)
{
linkedBinaryTree<E>::visit(t); //访问根节点
preOrder(t->leftChild); //前序遍历左子树
preOrder(t->rightChild); //前序遍历右子树
}
}
template <class E>
void linkedBinaryTree<E>::levelOrder(
void (*theVisit)(binaryTreeNode<E> *))
{ //层次遍历二叉树
binaryTreeNode<E> *t = root;
arrayQueue<binaryTreeNode<E> *> q;
while (t != NULL)
{
theVisit(t); //访问t
//将t的左右孩子放入队列
if (t->leftChild)
q.push(t->LeftChild);
if (t->rightChild)
q.push(t->rightChild);
try
{
t = q.front();
} //访问下一个节点 .
catch (queueEmpty)
{
return;
}
q.pop();
}
}
¶ 输出
private:
// ...
static void output(binaryTreeNode<E> *t)
{
cout << t->element << ' ';
}
public:
// ...
void preOrderOutput()
{
preOrder(output);
cout << endl;
}
void inOrderOutput()
{
inOrder(output);
cout << endl;
}
void postOrderOutput()
{
postOrder(output);
cout << endl;
}
void levelOutput()
{
levelOrder(output);
cout << endl;
}
¶ 计算高度
public:
int Height( ) const {return height (root);}
private:
int height (binaryTreeNode<E> *t) const;
template <class E>
int linkedBinaryTree<E>::height(BinaryTreeNode<E> *t)
{ //返回二叉树*t的高度
If(t == NULL) return 0; // 空树
int hl = height(t->leftChild); // 左子树的高度
int hr = height(t->rightChild); // 右子树的高度
if (hl > hr)
return ++hl;
else
return ++hr;
}
¶ 统计节点数量
先序(或中序或后序)遍历二叉树,在遍历过程中统计结点。由此,需在遍历算法中增添一个“计数”的参数,并将算法中“访问结点”的操作改为:计数器增1。
public:
int Size()
{
_count = 0;
PreOrder(Add1,root);
return _count;
}
private:
static void Add1(binaryTreeNode<T> *t) { _count++; }
只统计叶子节点的个数:
public:
int Size()
{
_count = 0;
PreOrder(Add2, root);
return _count;
}
private:
static void Add2(binaryTreeNode<T> *t)
{
if (!t->LeftChild && !t->RightChild)
_count++;
}
¶ 二叉树的复制
其基本操作为:生成一个结点。
进行 BFS 遍历。
¶ 最近公共祖先
求二叉树两节点的LCA(最近公共祖先)(必须要会+常考)+求叶子节点到LCA的距离+求两个叶子节点之间的距离:
¶ 优先队列
优先队列未必靠堆实现,使用线性表保存权重也可以做到。但是堆更快。
¶ 二叉堆
堆是一棵树,其每个节点都有一个键值,且每个节点的键值都大于等于/小于等于其父亲的键值。每个节点的键值都大于等于其父亲键值的堆叫做小根堆,否则叫做大根堆。
二叉堆是一棵二叉树,并且是完全二叉树,每个结点中存有一个元素(或者说,有个权值)。
¶ 插入
插入操作是指向二叉堆中插入一个元素,要保证插入后也是一棵完全二叉树。
最简单的方法就是,最下一层最右边的叶子之后插入。如果最下一层已满,就新增一层。
插入之后可能会不满足堆性质?
向上调整:如果这个结点的权值大于它父亲的权值,就交换,重复此过程直到不满足或者到根。
可以证明,插入之后向上调整后,没有其他结点会不满足堆性质。向上调整的时间复杂度是 的。
¶ 删除
删除操作指删除堆中最大的元素,即删除根结点。
但是如果直接删除,则变成了两个堆,难以处理。所以不妨考虑插入操作的逆过程,设法将根结点移到最后一个结点,然后直接删掉。然而实际上不好做,我们通常采用的方法是,把根结点和最后一个结点直接交换。于是直接删掉(在最后一个结点处的)根结点,但是新的根结点可能不满足堆性质……
向下调整:在该结点的儿子中,找一个最大的,与该结点交换,重复此过程直到底层。
可以证明,删除并向下调整后,没有其他结点不满足堆性质。时间复杂度 。
¶ 建堆
考虑这么一个问题,从一个空的堆开始,插入 个元素,不在乎顺序。直接一个一个插入需要 的时间
使用向上调整,需要的时间。
使用向下调整只需要。从叶子开始,逐个向下调整;换一种理解方法,每次「合并」两个已经调整好的堆,这说明了正确性。
¶ 左偏树
左偏树 与 配对堆 一样,是一种 可并堆,具有堆的性质,并且可以快速合并。
左偏树是一棵二叉树,它不仅具有堆的性质,并且是「左偏」的:每个节点左儿子的 都大于等于右儿子的 。因此,左偏树每个节点的 都等于其右儿子的 加一。
¶ 合并
合并两个堆时,由于要满足堆性质,先取值较小(为了方便,本文讨论小根堆)的那个根作为合并后堆的根节点,然后将这个根的左儿子作为合并后堆的左儿子,递归地合并其右儿子与另一个堆,作为合并后的堆的右儿子。为了满足左偏性质,合并后若左儿子的 小于右儿子的 ,就交换两个儿子。
¶ 应用)
¶ 堆排序
堆排序(英语:Heapsort)是指利用 二叉堆 这种数据结构所设计的一种排序算法。堆排序的适用数据结构为数组。堆排序的本质是建立在堆上的选择排序。
首先建立大顶堆,然后将堆顶的元素取出,作为最大值,与数组尾部的元素交换,并维持残余堆的性质;之后将堆顶的元素取出,作为次大值,与数组倒数第二位元素交换,并维持残余堆的性质;以此类推,在第 次操作后,整个数组就完成了排序。
从根节点开始,依次将每一层的节点排列在数组里。于是有数组中下标为 的节点,对应的父结点、左子结点和右子结点如下:
iParent(i) = (i - 1) / 2;
iLeftChild(i) = 2 * i + 1;
iRightChild(i) = 2 * i + 2;
¶ 霍夫曼编码
霍夫曼编码(Huffman code)是另外一种文本压缩算法,它根据不同符号在一段文字中的相对出现频率来进行压缩编码。
当每个字符出现的频率有很大变化时,可以通过可变长的编码来降低编码串的长度。当频率相差大时这种差别会更为明显。
若使用可变长编码,编码需要满足:没有任何一个代码是另一代码的前缀
霍夫曼树可用于构造 最短的前缀编码,即 霍夫曼编码(Huffman Code)
¶ 搜索树
平均搜索长度:
¶ 简介
搜索树(Search Trees) 是一种适合于描述字典的树形结构。
- 比跳表和散列表有更好或类似的性能
- 特别是对于顺序访问或按排名访问,散列表实现时间性能差,使用搜索树实现则会有更好的时间性能。
二叉搜索树是一棵可能为空的二叉树,一棵非空的二叉搜索树满足以下特征:
- 每个元素有一个关键字,并且没有任意两个元素有相同的关键字;因此,所有的关键字都是唯一的。
- 任何节点左子树的关键字小于该节点的关键字;任何节点右子树的关键字大于该节点的关键字。
索引二叉搜索树定义:
- 二叉搜索树
- 在每个节点中添加一个 ‘LeftSize’—该节点左子树的元素个数
- LeftSize(x):给出了一个元素在x为根的子树中排名(0起始)
¶ 搜索树的插入
若在二叉搜索树中插入一个新元素e,首先搜索,验证e 的关键值是否存在如果搜索成功,那么新元素将不被插入;如果搜索不成功,那么新元素将被插入到搜索的中断点。
¶ 搜索树的删除
二叉搜索树的插入有三种情况:叶子结点的删除、只有一棵子树结点的删除和有两棵子树结点的删除。
- 叶子结点的删除可以直接丢弃。
- 只有一棵子树结点:若该节点为根结点,直接丢弃;否则让其父节点指针指向该节点的唯一子节点。
- 有两棵子树结点的删除只需将该元素替换为它的左子树中的最大元素或右子树中的最小元素。
¶ 平衡搜索树
¶ AVL树
AVL 树,是一种平衡的二叉搜索树。由于各种算法教材上对 AVL 的介绍十分冗长,造成了很多人对 AVL 树复杂、不实用的印象。但实际上,AVL 树的原理简单,实现也并不复杂。
平衡因子:右子树高度 - 左子树高度。
AVL树相比于二叉搜索树,特点在于如果 T 是一棵 AVL 树,那么其左右子树也是 AVL 树,并且 , 是其左右子树的高度。为了维护这个性质,需要沿着从被插入/删除的节点到根的路径对树进行维护。
其插入时的调整有四种情况:
- LL
- LR
- RR
- RL
删除时根据直接父节点的平衡因子,有六种情况:
- R0
- R1
- R-1
- L0
- L1
- L-1
¶ 红黑树
¶ B树(P381)
在计算机科学中,B 树(B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。
由于三阶B树有两个或三个子节点,所以又被称为2-3树;同理四阶B树也被称为2-3-4树
AVL 树是特殊的二叉树,是最早被发明的自平衡二叉查找树。B 树保留了自平衡的特点,但 B 树的每个节点可以拥有两个以上的子节点,因此 B 树是一种多路搜索树。
设m叉搜索树的高度为,存在关系,搜索、插入和删除操作需要的磁盘访问次数为。为保证操作性能,必须确保高度值接近于。
m叉搜索树与m阶B树是不同的。
- B树要求每个内部节点至少有 个孩子。
- 根节点至少有2个孩子。
- 所有外部节点位于同一层上(因此B树是一棵满二叉树)。
对于B树,设,存在性质:
实际上,B树的序取决于磁盘块的大小和单个元素的大小。节点小于磁盘块的大小并无好处,这是因为每次磁盘访问只读或写一个块。节点大于磁盘块的大小会带来多重磁盘访问,每次磁盘访问都伴随一次搜索和时间延迟,因此节点大于磁盘块的大小也是不可取的。
-
搜索时,磁盘访问次数最多是。
-
删除时,最坏情况下磁盘访问次数是。
- 找到包含被删除元素的节点: 次读访问
- 获取第2至h 层的最相邻兄弟: 次读访问
- 在第3至h层的合并: 次写访问
- 对修改过的根节点和第2层的两个节点:次写访问。
¶ 图
¶ 图的存储
几种方法的复杂度比较(n为点数,m为边数):
| 方法 | 查询是否存在边 | 遍历点的所有出边 | 遍历整张图 | 空间复杂度 |
|---|---|---|---|---|
| 直接存边 | ||||
| 邻接矩阵 | ||||
| 邻接表 |
¶ 直接存边
使用一个数组来存边,数组中的每个元素都包含一条边的起点与终点(带边权的图还包含边权)。(或者使用多个数组分别存起点,终点和边权。)
class Edge:
u = 0
v = 0
n, m = map(lambda x:int(x), input().split())
e = [Edge()] * m; vis = [False] * n
for i in range(0, m):
e[i].u, e[i].v = map(lambda x:int(x), input().split())
def find_edge(u, v):
for i in range(1, m + 1):
if e[i].u == u and e[i].v == v:
return True
return False
def dfs(u):
if vis[u]:
return
vis[u] = True
for i in range(1, m + 1):
if e[i].u == u:
dfs(e[i].v)
由于直接存边的遍历效率低下,一般不用于遍历图。在 Kruskal 算法 中,由于需要将边按边权排序,需要直接存边。
在有的题目中,需要多次建图(如建一遍原图,建一遍反图),此时既可以使用多个其它数据结构来同时存储多张图,也可以将边直接存下来,需要重新建图时利用直接存下的边来建图。
¶ 邻接矩阵
使用一个二维数组 adj 来存边,其中 adj[u][v] 为 1 表示存在 u 到 v 的边,为 0 表示不存在。如果是带边权的图,可以在 adj[u][v] 中存储 u 到 v 的边的边权。
vis = [False] * (n + 1)
adj = [[False]] * (n + 1)
for i in range(1, m + 1):
u, v = map(lambda x:int(x), input().split())
adj[u][v] = True
def find_edge(u, v):
return adj[u][v]
def dfs(u):
if vis[u]:
return
vis[u] = True
for v in range(1, n + 1):
if adj[u][v]:
dfs(v)
邻接矩阵只适用于**没有重边(或重边可以忽略)**的情况。
其最显著的优点是可以 查询一条边是否存在。
由于邻接矩阵在稀疏图上效率很低(尤其是在点数较多的图上,通常可以以100个点为界,此时空间无法承受),所以一般只会在稠密图上使用邻接矩阵。
¶ 邻接表
使用一个支持动态增加元素的数据结构构成的数组,如 来存边,其中 存储的是点 的所有出边的相关信息(终点、边权等)。
vis = [False] * (n + 1)
adj = [[]] * (n + 1)
for i in range(1, m + 1):
u, v = map(lambda x:int(x), input().split())
adj[u].append(v)
def find_edge(u, v):
for i in range(0, len(adj[u])):
if adj[u][i] == v:
return True
return False
def dfs(u):
if vis[u]:
return
vis[u] = True
for i in range(0, len(adj[u])):
dfs(adj[u][i])
存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)。
尤其适用于需要对一个点的所有出边进行排序的场合。
¶ 图的遍历
通常,对图使用DFS为主,相应存储方式下的DFS实现在上文已经给出,这里仅补充BFS。
从一个顶点开始,识别所有可到达顶点的方法叫作宽度优先搜索 (Breadth -FirstSearch, BFS)。这种搜索可使用队列来实现。
叙述图的深度优先遍历和宽度优先遍历中,堆栈和队列的作用:
- 深度优先搜索算法是先访问根节点,接着遍历左子树再遍历右子树。因为栈是后进先出的结构,先将右子树压栈,再将左子树压栈,这样左子树就位于栈顶,可以保证先遍历左子树再遍历右子树。
- 一层一层遍历的,所以使用队列这种数据结构,先将一层节点放到队列中,当遍历完当前这一层后,再分别出队列,同时遍历当前节点的子节点,达到一层一层遍历的目的。若使用栈,压入第二层时,出栈就无法按照正常顺序输出了。
¶ 链式前向星
本质上是用链表实现的邻接表
¶ 拓扑排序(P428)
拓扑排序要解决的问题是给一个图的所有节点排序。拓扑排序的目标是将所有节点排序,使得排在前面的节点不能依赖于排在后面的节点。
我们可以拿大学选课的例子来描述这个过程,比如学习大学课程中有:单变量微积分,线性代数,离散数学概述,概率论与统计学概述,语言基础,算法导论,机器学习。当我们想要学习 算法导论 的时候,就必须先学会 离散数学概述 和 概率论与统计学概述,不然在课堂就会听的一脸懵逼。当然还有一个更加前的课程 单变量微积分。这些课程就相当于几个顶点 , 顶点之间的有向边 就相当于学习课程的顺序。显然拓扑排序不是那么的麻烦,不然你是如何选出合适的学习顺序。下面将介绍如何将这个过程抽象出来,用算法来实现。
但是如果某一天排课的老师打瞌睡了,说想要学习 算法导论,还得先学 机器学习,而 机器学习 的前置课程又是 算法导论,然后你就一万脸懵逼了,我到底应该先学哪一个?当然我们在这里不考虑什么同时学几个课程的情况。在这里,算法导论 和 机器学习 间就出现了一个环,显然你现在没办法弄清楚你需要学什么了,于是你也没办法进行拓扑排序了。因而如果有向图中存在环路,那么我们就没办法进行 拓扑排序 了。
初始状态下,集合 装着所有入度为 的点, 是一个空列表。每次从 中取出一个点 (可以随便取)放入 , 然后将 的所有边 删除。对于边 ,若将该边删除后点 的入度变为 ,则将 放入 中。
不断重复以上过程,直到集合 为空。检查图中是否存在任何边,如果有,那么这个图一定有环路,否则返回 , 中顶点的顺序就是拓扑排序的结果。
拓扑排序需要遍历所有节点初始化度数,并在排序过程中遍历所有的边,所以复杂度为 。
Kahn(BFS)实现:
int n, m;
vector<int> G[MAXN];
int in[MAXN]; // 存储每个结点的入度
bool toposort() {
vector<int> L;
queue<int> S;
for (int i = 1; i <= n; i++)
if (in[i] == 0) S.push(i);
while (!S.empty()) {
int u = S.front();
S.pop();
L.push_back(u);
for (auto v : G[u]) {
if (--in[v] == 0) {
S.push(v);
}
}
}
if (L.size() == n) {
for (auto i : L) cout << i << ' ';
return true;
} else {
return false;
}
}
from enum import Enum, auto
class Status(Enum):
to_visit = auto()
visiting = auto()
visited = auto()
def topo_sort(graph: list[list[int]]) -> list[int] | None:
n = len(graph)
status = [Status.to_visit] * n
order = []
def dfs(u: int) -> bool:
status[u] = Status.visiting
for v in graph[u]:
if status[v] == Status.visiting:
return False
if status[v] == Status.to_visit and not dfs(v):
return False
status[u] = Status.visited
order.append(u)
return True
for i in range(n):
if status[i] == Status.to_visit and not dfs(i):
return None
return order[::-1]
¶ 最短路问题
¶ Floyd
Floyd算法是用来求任意两个结点之间的最短路的。复杂度比较高,但是常数小,容易实现。
适用于任何图,不管有向无向,边权正负,但是最短路必须存在。(不能有个负环)。
我们定义一个数组 f[k][x][y],表示只允许经过结点 1 到 k(也就是说,在子图 中的路径,注意, 与 不一定在这个子图中),结点 到结点 的最短路长度。
很显然,f[n][x][y] 就是结点 到结点 的最短路长度(因为 即为 本身,其表示的最短路径就是所求路径)。
接下来考虑如何求出 f 数组的值。
f[0][x][y]: 与 的边权,或者 ,或者 (f[0][x][y] 什么时候应该是 ?当 与 间有直接相连的边的时候,为它们的边权;当 的时候为零,因为到本身的距离为零;当 与 没有直接相连的边的时候,为 )。
f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k]+f[k-1][k][y])(f[k-1][x][y],为不经过 点的最短路径,而 f[k-1][x][k]+f[k-1][k][y],为经过了 点的最短路)。
上面两行都显然是对的,所以说这个做法空间是 ,我们需要依次增加问题规模( 从 到 ),判断任意两点在当前问题规模下的最短路。
for k in range(1, n + 1):
for x in range(1, n + 1):
for y in range(1, n + 1):
// 相当于进行松弛操作
f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y])
¶ Dijkstra
Dijstra是一种求解非负权图上单源最短路径的算法。
将结点分成两个集合:已确定最短路长度的点集(记为 集合)的和未确定最短路长度的点集(记为 集合)。一开始所有的点都属于 集合。
初始化 ,其他点的 均为 。
然后重复这些操作:
- 从 集合中,选取一个最短路长度最小的结点,移到 集合中。
- 对那些刚刚被加入 集合的结点的所有出边执行松弛操作。
直到 集合为空,算法结束。
有多种方法来维护 1 操作中最短路长度最小的结点,不同的实现导致了 Dijkstra 算法时间复杂度上的差异。
- 暴力:不使用任何数据结构进行维护,每次
2操作执行完毕后,直接在 集合中暴力寻找最短路长度最小的结点。2操作总时间复杂度为 ,1操作总时间复杂度为 ,全过程的时间复杂度为 。 - 二叉堆:每成功松弛一条边 ,就将 插入二叉堆中(如果 v 已经在二叉堆中,直接修改相应元素的权值即可),
1操作直接取堆顶结点即可。共计 次二叉堆上的插入(修改)操作, 次删除堆顶操作,而插入(修改)和删除的时间复杂度均为 ,时间复杂度为 。 - 优先队列:和二叉堆类似,但使用优先队列时,如果同一个点的最短路被更新多次,因为先前更新时插入的元素不能被删除,也不能被修改,只能留在优先队列中,故优先队列内的元素个数是 的,时间复杂度为 )。
- Fibonacci 堆:和前面二者类似,但 Fibonacci 堆插入的时间复杂度为 ,故时间复杂度为 ,时间复杂度最优。但因为 Fibonacci 堆较二叉堆不易实现,效率优势也不够大,算法竞赛中较少使用。
- 线段树:和二叉堆原理类似,不过将每次成功松弛后插入二叉堆的操作改为在线段树上执行单点修改,而
1操作则是线段树上的全局查询最小值。时间复杂度为 。
在稀疏图中,,使用二叉堆实现的 Dijkstra 算法较 Bellman-Ford 算法具有较大的效率优势;而在稠密图中,,这时候使用暴力做法较二叉堆实现更优。
暴力实现:
class Edge:
v = 0
w = 0
e = [[Edge() for i in range(maxn)] for j in range(maxn)]
dis = [63] * maxn; vis = [] * maxn
def dijkstra(n, s):
dis[s] = 0
for i in range(1, n + 1):
u = 0
mind = 0x3f3f3f3f
for j in range(1, n + 1):
if vis[j] == False and dis[v] < mind:
u = j
mind = dis[j]
vis[u] = True
for ed in e[u]:
v, w = ed.v, ed.w
if dis[v] > dis[u] + w:
dis[v] = dis[u] + w
¶ 最小生成树
我们定义无向连通图的 最小生成树(Minimum Spanning Tree,MST)为边权和最小的生成树。
注意:只有连通图才有生成树,而对于非连通图,只存在生成森林。
¶ Kruskal算法
Kruskal 算法是一种常见并且好写的最小生成树算法,由 Kruskal 发明。该算法的基本思想是从小到大加入边,是个贪心算法。
算法虽简单,但需要相应的数据结构来支持……具体来说,维护一个森林,查询两个结点是否在同一棵树中,连接两棵树。抽象一点地说,维护一堆集合,查询两个元素是否属于同一集合,合并两个集合。其中,查询两点是否连通和连接两点可以使用并查集维护。
如果使用 的排序算法,并且使用 或 的并查集,就可以得到时间复杂度为 的 Kruskal 算法。
Kruskal算法中,如何判定是否存在回路?两个顶点是否在同一个集合中可利用并查集中的find操作实现,若两个顶点在同一个集合中,那么假如这条边就会形成回路;与此同时,每次添加新的边时需要进行unite操作。
¶ Prim算法
Prim 算法是另一种常见并且好写的最小生成树算法。该算法的基本思想是从一个结点开始,不断加点(而不是 Kruskal 算法的加边)。
具体来说,每次要选择距离最小的一个结点,以及用新的边更新其他结点的距离。其实跟 Dijkstra 算法一样,每次找到距离最小的一个点,可以暴力找也可以用堆维护。
堆优化的方式类似 Dijkstra 的堆优化,但如果使用二叉堆等不支持 decrease-key 的堆,复杂度就不优于 Kruskal,常数也比 Kruskal 大。所以,一般情况下都使用 Kruskal 算法,在稠密图尤其是完全图上,暴力 Prim 的复杂度比 Kruskal 优,但 不一定 实际跑得更快。
不同实现下,其性能可以分别达到:
- 暴力:。
- 二叉堆:。
- Fib 堆:。
¶ Boruvka 算法
Boruvka 算法的思想是前两种算法的结合。它可以用于求解 边权互不相同 的无向图的最小生成森林。(无向连通图就是最小生成树。)
¶ 贪婪算法
贪心算法(英语:greedy algorithm),是用计算机来模拟一个「贪心」的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
¶ 最优化问题
¶ 分治
分治(英语:Divide and Conquer),字面上的解释是「分而治之」,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
递归是一种编程技巧,一种解决问题的思维方式;分治算法很大程度上是基于递归的,解决更具体问题的算法思想。
分治算法的核心思想就是「分而治之」。大概的流程可以分为三步:分解一>解决一>合并。
- 分解原问题为结构相同的子问题。
- 分解到某个容易求解的边界之后,进行递归求解。
- 将子问题的解合井成原问题的解。
分治法能解决的问题一般有如下特征:
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若千个规模较小的相同问题,即该问题具有最优子结构性质,利用该问题分解出的子问题的解可以合井为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
¶ 动态规划
¶ 典型问题
¶ 树的计算
¶ 二叉树的数值
¶ B-树
对一个m阶B树:
- 每个节点至多有 个子节点,也就是m-1个键
- 除根节点、叶子结点以外的节点最少有 个子节点,也就是 个键。
- 根节点有至少两个子节点,也就是一个键
- 每个节点至多包含 个键 ????
含有n个非叶结点的m阶B-树中至少包含多少个关键字?
n个非叶结点中,根节点至少有一个关键字;其他 各节点各自至少有 个关键字,总共有 个关键字。
¶ 排序算法
- 基数排序、计数排序、插入排序、冒泡排序、归并排序是稳定排序。
- 选择排序、堆排序、快速排序、希尔排序不是稳定排序。
插入、选择和冒泡是复杂度的算法。
¶ 拓扑排序
¶ 归并排序
归并排序(merge sort)是高效的基于比较的稳定排序算法。
归并排序基于分治思想将数组分段排序后合并,时间复杂度在最优、最坏与平均情况下均为 ,空间复杂度为 。归并排序可以只使用 的辅助空间,但为便捷通常使用与原数组等长的辅助数组。
¶ 搜索算法
¶ 等价类与并查集
- 离线等价类问题:已知n和R,确定所有的等价类
- 在线等价类问题(又称为并查集问题):初始有n个元素,每个元素都属于一个独立的等价类
并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
- 合并(Union):把两个不相交的集合合并为一个集合。
- 查询(Find):查询两个元素是否在同一个集合中。
¶ 离线等价类
实现离线等价类需要如下部分:
- 一个长度为 的链表数组,用于保存每个元素的关系。
- 一个栈,用于在输出时保存回溯信息。
- 一个布尔数组,用于输出时保存元素是否被输出过。

